をGIHOZで解いてみるシリーズです。
GIHOZはこちら>テスト技法ツールGIHOZ(ギホーズ)|ソフトウェアテスト・第三者検証のベリサーブ
GIHOZ(ギホーズ)は、各種テスト技法を手軽に利用できるクラウド型ツールです。
記事執筆時点で無料なので、誰でも(アカウント作れば)触れます。
また、GIHOZは自分がテスト技法使って作った成果物をGIHOZ上で一般公開できるので、以下のURLにアクセスしていただければ私がGIHOZで練習問題解いた解答が見られます。
問題と私の解答
【問題5】境界値分析☆☆
【問題5】境界値分析☆☆
— あきやま🍵 (@akiyama924) March 12, 2017
2017年4月に小学校入学する(小学1年生になる)子供について、境界値分析によって求めたテストすべき生年月日として最も適当なものを下記から選択しなさい。
生年月日を表すのにムリがあった・・・ので頭で解きます。
2017/4/1に小学校に入学するということは、7歳になる歳、ということです。
- 2017年度に7歳
- 2016年度に6歳
- 2015年度に5歳
- 2014年度に4歳
- 2013年度に3歳
- 2012年度に2歳
- 2011年度に1歳
- 2010年度に0歳=2010年度生まれ
と愚直に書き出してみたほうが凡ミスがなさそうです。
で、小学校の入学する生年月日は実は4/1ではなく4/2からなので、2017/4/1に小学校入学する子供の生年月日の範囲は、2010/4/2~2011/4/1となります。
よって、②。正解!
【問題6】境界値分析☆☆☆
選択肢
— あきやま🍵 (@akiyama924) March 13, 2017
① 暖房:9,10,25,26、冷房:14,15,30,31
② 暖房冷房とも:9,10,14,15,25,26,30,31
③ 暖房:9,10,14,15,25,26、冷房:14,15,25,26,30,31
④ 暖房冷房とも:14,15,25,26
GIHOZで冷房時の温度と暖房時の温度同時に考えられるんだろうか・・・と思ったものの、数直線2本使えました。これは良い。
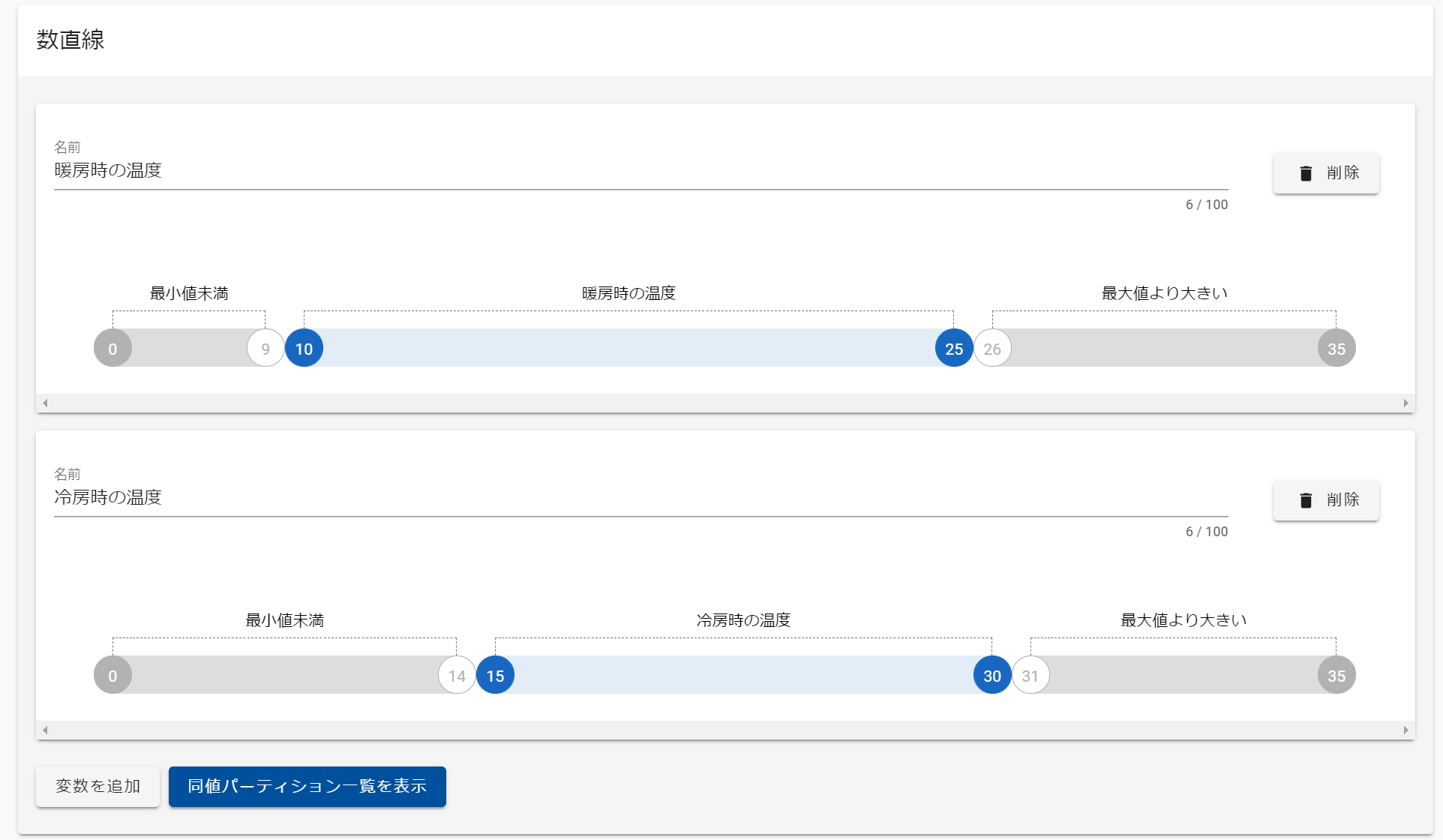
ここからテストケース生成した結果が以下
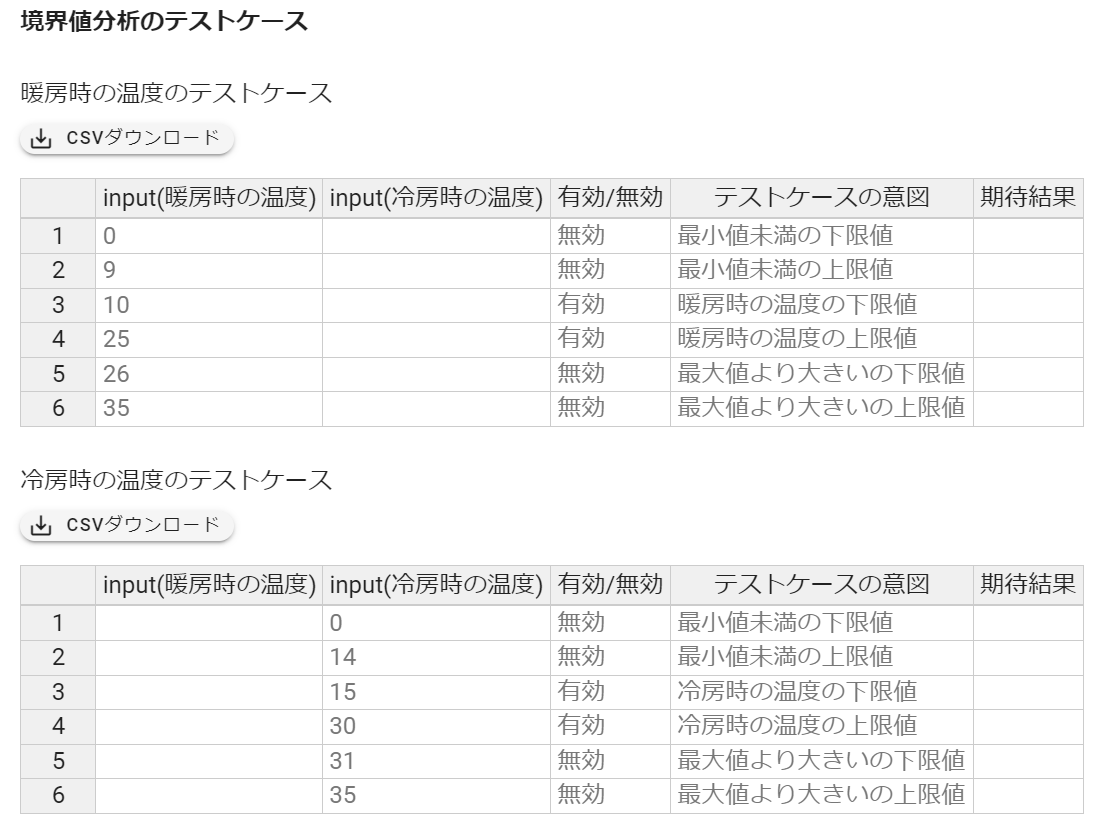
ということで答えは①・・・と思ったのですが、正解は③でした。
この問題については☆が3つの難易度ということで、ツイートの続きで秋山さんの解説があります。
設定温度の境界値を求める問題ですので、まずは、設定温度の同値分割をする必要があります。 x 〜9℃:無効同値クラス 10〜14℃:暖房の有効同値クラス 15〜25℃:暖房・冷房共有効同値クラス 26〜30℃:冷房の有効同値クラス 31〜y℃:無効同値クラス
です。
x℃とy℃については情報がありません。でも、どちらも無効同値クラスの端で直接に値を入力出来そうに無いことからテストは不要と判断します。 問題文に温度設定の方法が書いてありませんので常識から判断するしかありませんが、デフォルト値で動き出して△▽ボタンで変えるタイプでしょう。
あとは、見つかった境界値を暖房と冷房でできるだけテストするようにします。 そうすると、選択肢3となります。
このへんがしっくりこずでした・・・。まだまだです。
と、こんな感じで2,3問ずつ頭の体操とGIHOZの使い方を覚えることを兼ねて、こつこつやってみようと思います。次からはデシジョンテーブル。